Claude Code and Stan Splines

My previous experience with statistical modelling is mostly with mgcv's GAMs .(Generalized Additive Models). These GAMs are a form of regression modelling where the explanatory variables of the regression are transformed with a flexible function that is 'learned' during model fitting. Combined with some form of regularisation to avoid extreme overfitting, these flexible functions are very useful to recover the shape of a non-linear process. An example would be fitting a seasonal growth component in a vector species in a disease, but for which you don't know when its seasonal peak is. 

Besides GAM modeling, I have done some brms modeling when trying to model more complex plague spillover models which needed hurdle or zero-inflation models that were not part of the mgcv package. This work unfortunately never got published: the foreign data owner suddenly went quiet, and we didn't have contracts in place - lesson learned! Nevertheless, applying these brms or GAM models on a complex spillover dataset was a highly valuable learning experience and a very nice complement to my experience in building mechanistic disease models.

Using mgcv, I got familiar and fond of using splines to model unknown non-linear processes. And now, with a project in stan, I wanted to fall back to using splines as well.

Splines in stan have been build and explored before, and come in two flavors. The implementations I used here are those of Milad Kharratzadeh for B-splines (Splines-in-Stan) and of Sergey Koposov for C-splines (stan-splines). The two splines differ in some characteristics, but are both capable of estimating the smooth transform functions. If you want a heuristic of the difference: the b-spines split up the x-axis in many small segments (called knots) that are correlated together with a smoothing parameter to avoid overfitting, while the cubic splines allow a wiggly line a limited number of turns (also called knots), and you control the smoothing by allowing more or less knots.

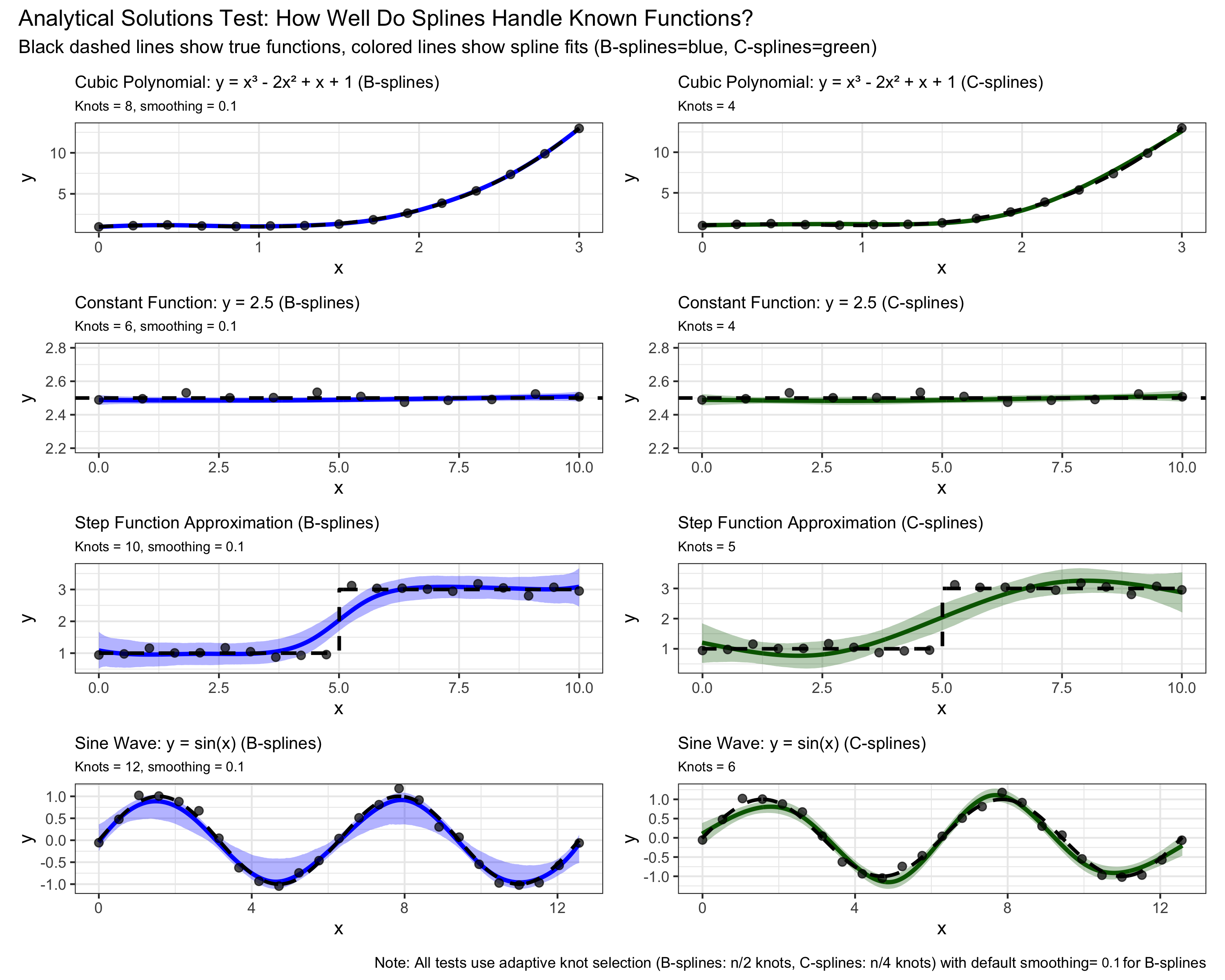
I tried to let Claude Code plug them into my existing stan model, based on the examples available on the web and on github. It felt better, however, to first implement both B-splines and C-splines in a separate project where I could evaluate and understand them, without immediately plugging them into a more complex project. Especially when using Claude Code, there is a real need to scrutinize and understand the code that is generated!

So that is this project. It is available here: https://github.com/BorisVSchmid/blog-stan_with_splines/. It pulls together the implementations for B-splines and C-splines, explores evaluation of the spline fits and options to make the smoothing parameter of the B-splines scale with dataset-size and have smoothing start at 0 for no smoothing (and high smoothing is already at 0.2). It is also built with heavy help of Claude Code, which is why I spend quite some time to also include tests and examples to find edge cases or correct overly complex code constructs. It is the first project I've build with a command-line LLM assisting, and we are both learning :-).

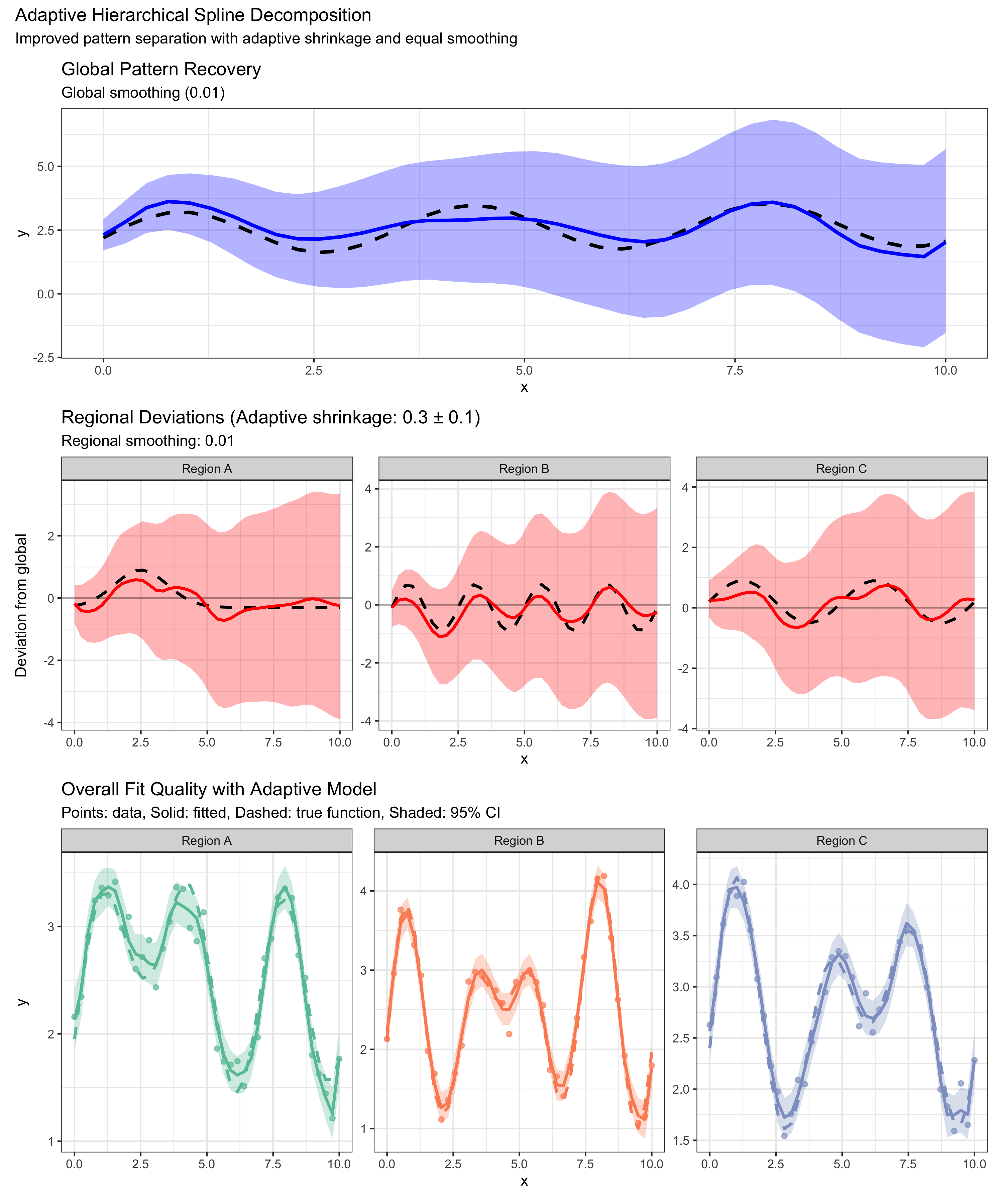
After testing the spline implementations, I ended this project with a hierarchical example of a global function and three regional functions that the splines needed to disentangle. This was close to how I intended to use splines in a research project. Funny thing, I ended up not using splines at all for this project, but it was still a nice exercise.